Java Decorator Pattern은 객체 지향 디자인 패턴 중 하나로, 기본 기능에 추가할 수 있는 기능의 종류가 많은 경우에 각 추가 기능을 Decorator클래스로 정의 한 후 필요한 Decorator 객체를 조합함으로써 추가 기능의 조합을 설계 하는 방식이다.
Decorator 패턴은 기존 객체를 감싸는 새로운 데코레이터 클래스를 만들어서 기존 객체의 메소드를 호출하는 방식으로 동작합니다.이 패턴을 사용하면 기존 객체에 새로운 기능을 추가하기 위해 상속을 사용하는 대신, 런타임 시간에 객체의 기능을 동적으로 조작할 수 있습니다. 또한 여러 개의 데코레이터를 순차적으로 적용하여 새로운 기능을 더욱 다양하게 추가할 수 있습니다.
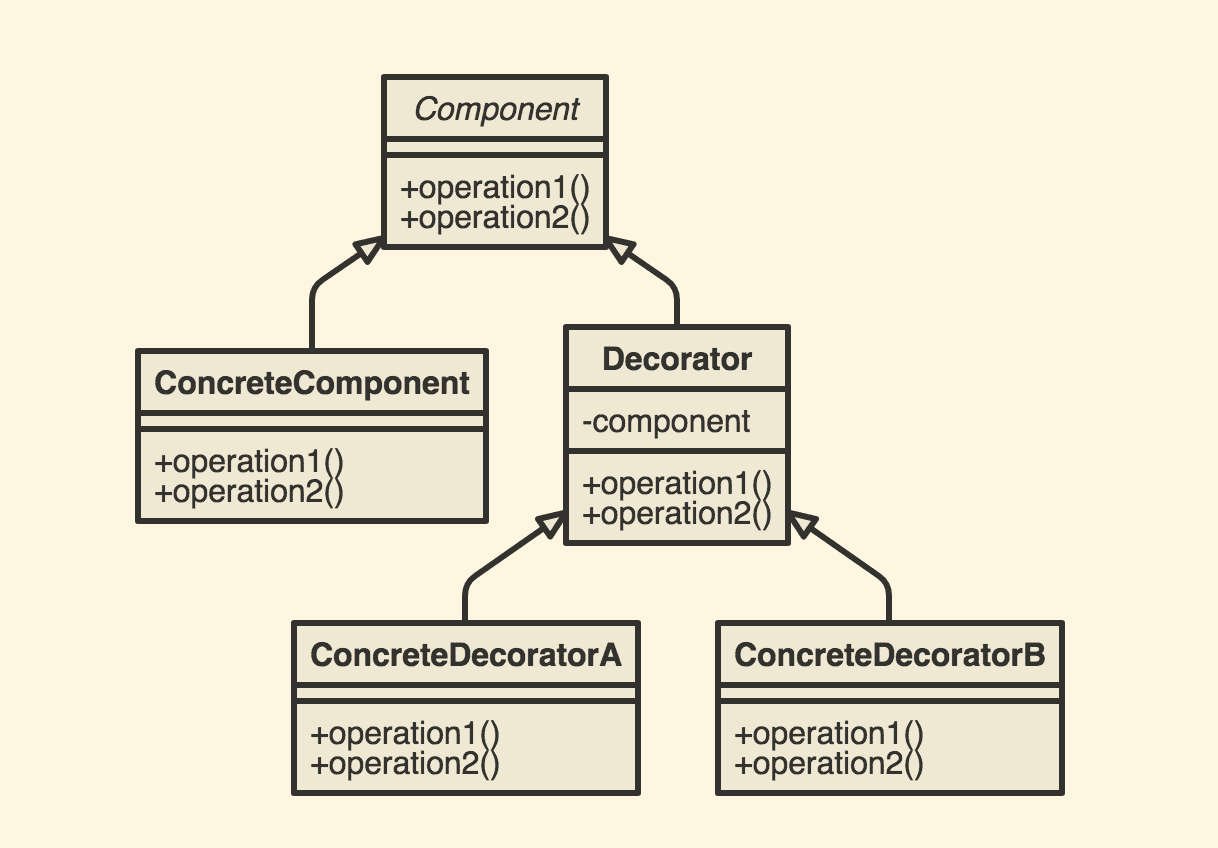
Java Decorator Pattern의 구성요소는 다음과 같습니다.
- Component: Decorator 패턴의 기초가 되는 인터페이스 또는 추상 클래스. Decorator 클래스와 ConcreteComponent 클래스가 이를 구현하게 됩니다.
- ConcreteComponent: Component의 구현체로서, 기본적인 기능을 제공하는 클래스입니다.
- Decorator: Component를 상속받는 추상 클래스로, 새로운 기능을 추가하기 위한 필드와 메소드를 가지고 있습니다. 또한 Component를 상속받는 모든 데코레이터 클래스의 공통점을 정의합니다.
- ConcreteDecorator: Decorator를 상속받는 실제 데코레이터 클래스로, 기존 객체에 새로운 기능을 추가합니다.
이렇게 구성된 Decorator 패턴은 객체 지향의 다형성을 이용하여 기존 객체에 새로운 기능을 추가하고 확장할 수 있으며, 코드의 유연성과 확장성을 높여줍니다.
// Component interface
public interface Coffee {
String getDescription();
double cost();
}
// Concrete Component
public class BasicCoffee implements Coffee {
@Override
public String getDescription() {
return "Basic coffee";
}
@Override
public double cost() {
return 2.0;
}
}
// Decorator
public abstract class CoffeeDecorator implements Coffee {
private Coffee decoratedCoffee;
public CoffeeDecorator(Coffee decoratedCoffee) {
this.decoratedCoffee = decoratedCoffee;
}
@Override
public String getDescription() {
return decoratedCoffee.getDescription();
}
@Override
public double cost() {
return decoratedCoffee.cost();
}
}
// Concrete Decorator
public class Milk extends CoffeeDecorator {
public Milk(Coffee decoratedCoffee) {
super(decoratedCoffee);
}
@Override
public String getDescription() {
return super.getDescription() + ", with milk";
}
@Override
public double cost() {
return super.cost() + 0.5;
}
}
// Concrete Decorator
public class Sugar extends CoffeeDecorator {
public Sugar(Coffee decoratedCoffee) {
super(decoratedCoffee);
}
@Override
public String getDescription() {
return super.getDescription() + ", with sugar";
}
@Override
public double cost() {
return super.cost() + 0.25;
}
}
// Client code
public class CoffeeShop {
public static void main(String[] args) {
Coffee basicCoffee = new BasicCoffee();
System.out.println(basicCoffee.getDescription() + ": " + basicCoffee.cost());
Coffee milkCoffee = new Milk(basicCoffee);
System.out.println(milkCoffee.getDescription() + ": " + milkCoffee.cost());
Coffee sugarCoffee = new Sugar(basicCoffee);
System.out.println(sugarCoffee.getDescription() + ": " + sugarCoffee.cost());
Coffee milkSugarCoffee = new Milk(new Sugar(basicCoffee));
System.out.println(milkSugarCoffee.getDescription() + ": " + milkSugarCoffee.cost());
}
}위 코드는 Coffee 인터페이스를 구현한 BasicCoffee 클래스와 CoffeeDecorator 추상 클래스를 정의하고, 이를 상속받아 구체적인 데코레이터 클래스인 Milk와 Sugar를 구현합니다. 각 데코레이터 클래스에서는 커피의 설명과 가격을 반환할 때 super 키워드를 이용해 기존 커피 객체의 설명과 가격을 먼저 가져오고, 이에 추가적인 설명과 가격을 더해줍니다. 마지막으로 클라이언트 코드에서는 다양한 데코레이터 객체를 조합하여 원하는 커피를 생성할 수 있습니다.
'알고리즘과 디자인패턴' 카테고리의 다른 글
| 알고리즘 관련 to know list (0) | 2022.03.29 |
|---|---|
| 리스트 정렬하기 (0) | 2022.01.23 |
| 자바로 구현한 병합 정렬 알고리즘 (merge sort) (0) | 2021.12.07 |
| 자바 알고리즘 스터디 (0) | 2021.08.11 |